Anatomy of a Useless Program

I’m sure we’ve all been here, just staring at a list of numbers on the screen of your Apple //e, thinking “Man… I wish I knew the sum of those numbers. I know it’s less than 65,535, none of them are negative, and gee whiz, I just don’t want to open the calculator app on my smartphone.” Well, consider this age-old problem solved. Just load this handy program on an Apple II-formatted 5.25" floppy disk and type BRUN sum whenever you need it. Here it is in action:

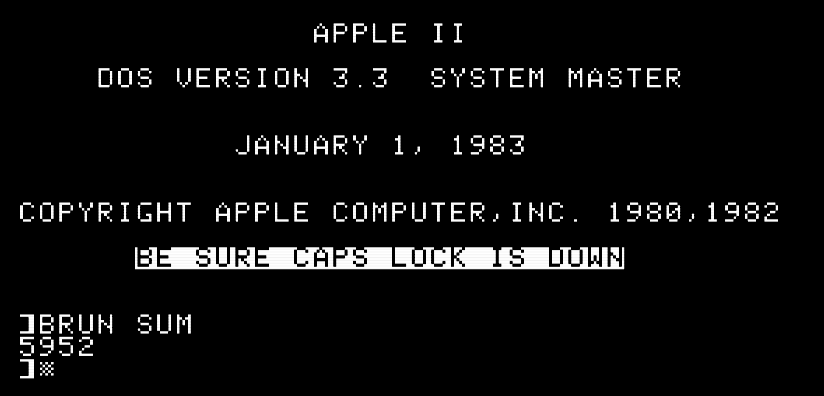
OK, so maybe, this program is useless, but it was fun to write and touched on problems that I don’t often consider, so I think we can learn from it. After all, even though a lot has changed in 40+ years, programming is still programming. The fundamentals are the same, and they will be the same as long as we have binary computers. So let’s dissect this program, even if it is useless.

A quick note about the scope of this article. I assume you don’t actually care about the Apple II or 6502 Assembly code, so I will focus on the fundamentals that have not changed, but some details are unavoidable.

If you want to run any of the code in this post, I tested the application using microM8 and an Enhanced Apple //e. It should work on later Apple II models, but I have liberally used 65(C)02 instructions, so it will not run on earlier models.¹

Finding digits

Our first task is to scan the Apple II’s video memory looking for ASCII digits (character codes 0x30 to 0x39). Here is the shell of our program, which handles that.

        org $800
page    equ $40     ; zero-page location of the page pointer

main
    ldy #0          ; Y will count up 0 to 255
    ldx #4          ; X will count down 4 to 1

    lda #0          ; lsb of page pointer is always 0
    sta page
    lda #$04        ; msb of page pointer, start at $400
    sta page+1
loop
    lda (page),Y    ; get digit at index Y
    and #$7f        ; ignore high bit
    sec             ; set carry before subtract
    sbc #$30        ; subtract ASCII 0 to get a digit

    bmi nonDigit    ; if the "digit" is less than 0
    cmp #10         ; compare to decimal 10
    bcs nonDigit    ; if A > 9

digit
    ; TODO: Handle a digit

nonDigit
    ; TODO: Handle a non-digit

next
    iny             ; go to the next character
    bne loop        ; if we did not overflow

nextPage
    dex             ; end of a page, decrecrment X
    beq end         ; if X is zero then we are done

    inc page+1      ; increment msb of the page counter
    bra loop        ; do it again

    rts             ; exit

The interesting code is after the loop label. ASCII only needs 7 bits, so computer designers had an extra bit that could be used however they wanted. The Apple II used it as a flag for inverse mode (black characters on a white background), but the differnce is irrelevant for this program, so we strip the high bit: and #$7f². If you haven’t worked with bitmasks before, this is what happens:

  10110111  = 0xb7, ASCII 7 (high bit set)
& 01111111  = 0x7f
----------
  00110111  = 0x37, ASCII 7 (high bit clear)

Now we have an ASCII character code, but we need to tell if it’s a digit. To decide, we subtract 0x30 (the ASCII code for 0) and check if the result is between 0 and 9.

Converting digits to numbers

Outside of one particularly impoverished templating language, I have always had access to a function that converted a string of digits to a number: str in Python, strconv.Atoi in Go, or even languages that implicitly convert strings to numbers (Perl). But the Apple II is no help here, we have to write it ourselves.

Even if you are unfamiliar with the algorithm to convert an ASCII string to a number, you could probably work it out in a few minutes with nothing more than your memory of grade school arithmetic, but here it is in Python anyway:

def atoi(s):
    result = 0
    for digit in s:
        n = ord(digit) - ord('0')
        if n < 0 or n > 9:
            raise Exception(
                f'"{digit}" is not a digit'
            )
        result = result * 10 + n
    return result

For every character, we subtract by 0x30 to get the value of the digit. Then we multiply the total by ten and add the digit.

Here it is in Assembly:

digit
    phx        ; save X
    phy        ; save Y

    ldx curr   ; copy lsb to X for multiply
    ldy curr+1 ; copy msb to Y for multiply
    jsr mul10  ; multiply by 10
    stx curr   ; store lsb of mul10 result
    sty curr+1 ; store msb of mul10 result

    ply        ; restore Y
    plx        ; restore X

    clc        ; clear carry before add
    adc curr   ; add digit to lsb
    sta curr   ; store digit in lsb
    lda #0     ; clear A to add carry
    adc curr+1 ; add carry to msb
    sta curr+1 ; store msb
    bra next   ; process the next character

This is equivalent to result = result * 10 + n in the Python version. We will discuss jsr mul10 in the next section.

curr is a pointer to two bytes of memory which stores the number we are building. It would be simpler to use just one byte for the answer, but that would be an extra useless program that could only add numbers up to 255.

Our 2-byte number is encoded in little-endian: the least-significant byte is stored first, followed by the most-significant byte. For example, 0x1234 would be 34 12 in memory.³

If, for some reason, you memorized addition facts up to 255, you could add numbers with pencil and paper just like a computer does. You would add the least-significant byte, mark the carry, then add the most-significant bytes with the carry. Here is an example:

  FF 12  = 0x12FF
+ 02 00  = 0x0002
-------
  00 13  = 0x1301

This is the same process for multi-byte addition the program does with the adc instructions. We could extend this for bigger numbers, but 65,535 seems like the appropriate level of uselessness.

Multiplication

The 6502 does not have an instruction for multiplication or division. The closest we have are shift instructions, which push the bits in a number to the left or right. This has the effect of either multiplying or dividing by 2. But that doesn’t help to multiply by 10, so we must write our own routine.

Multiplying binary numbers by hand is mostly the same method you probably had drilled into you early in your education for decimal numbers. Except binary numbers are much easier because the multiplication table is very tiny:

* | 0 | 1 |
0 | 0 | 0 |
1 | 0 | 1 |

Everything is 0 except for 1 x 1, and there is no carry. Here is a problem worked out:

    1111011 = 123
  x    1010 = 10
  ---------
    0000000
   1111011
  0000000
 1111011
-----------
10011001110 = 1230

This translates into code fairly easily, as long as the product is calculated as we go instead of saving the addition for the end. The algorithm goes like this to calculate p = a * b for unsigned integers:

• examine the right-most bit of a, if it’s one add b to p.
• shift b to the left (add a placeholder)
• shift a to the right
• repeat until a is 0

Here it is in Python:

def multiply(a, b):
    p = 0
    while a > 0:
        if a & 1:
            p += b
        a >>= 1
        b <<= 1
    return p

That can be almost directly translated to Assembly. But we can do a little better for our case because we only need to multiply by 10. Slightly later in grade school, you probably had Algebra and learned that 10x = 2x + 8x. That fact simplifies our task because we can multiply by 2 with a left shift. Here is the (unfortunately repetitive) code for mul10:

mul10
    pha        ; Save old A value

    ; Multiply by 2, and store the result
    txa        ; Copy lsb to A
    asl A      ; Multiply lsb by 2
    sta temp   ; Store lsb
    tya        ; Copy msb to A
    rol A      ; Multiply msb by 2
    sta temp+1 ; Store msb

    ; Multiply by 2, keep the result in X and Y
    txa        ; Copy lsb to A
    asl A      ; Multiply lsb by 2
    tax        ; Put lsb back in X
    tya        ; Copy msb to A
    rol A      ; Multiply msb by 2
    tay        ; Put msb back in Y

    ; Repeat for 4 times
    txa        ; Copy lsb to A
    asl A      ; Multiply lsb by 2
    tax        ; Put lsb back in X
    tya        ; Copy msb to A
    rol A      ; Multiply msb by 2
    tay        ; Put msb back in Y

    ; Repeat for 8 times
    txa        ; Copy lsb to A
    asl A      ; Multiply lsb by 2
    tax        ; Put lsb back in X
    tya        ; Copy msb to A
    rol A      ; Multiply msb by 2
    tay        ; Put msb back in Y

    ; Find 2x + 8x
    txa        ; Copy lsb to A
    clc        ; Clear carry before add
    adc temp   ; Add 2x + 8x in lsb
    tax        ; Store lsb in X
    tya        ; Copy msb to A
    adc temp+1 ; Add 2x + 8x in msb
    tay        ; Store msb in Y

    pla        ; Restore A
    rts

The keys here are the asl (arithmetic shift left) and rol (rotate left) instructions. asl shifts a byte one bit to the left, removing the left-most bit from the number and pushing a 0 in the right. If that left-most bit was 1, then the carry flag will be set. rol works the same, except that instead of pushing a 0, it uses the value of the carry flag. This enables multi-byte shifts, much like we saw with multi-byte addition.

If you want more about multiplying numbers with the 6502, Neil Parker has a detailed article on the subject.

Adding it up

Now that we found the numbers, we can perform the more straightforward task of adding up the total.

...

nonDigit
    phx         ; save X
    lda curr    ; get lsb of the current number
    ldx curr+1  ; get msb of the current number
    bne notZero ; if msb is not zero
    cmp #0      ; if lsb is not zero
    bne notZero

    plx         ; current is zero, pop x
    bra next    ; go to the next number

notZero
    clc         ; clear carry before add
    adc total   ; add lsb of current to the total
    sta total   ; store lsb of the current total
    txa         ; copy msb from X to A
    adc total+1 ; add msb of current to the total
    sta total+1 ; store msb of the current total

    plx         ; restore X

    lda #0      ; clear current
    sta curr
    sta curr+1

...

When we find the end of a string of digits, we add curr to total. In most other languages, this would be total += curr followed by curr = 0.

Converting a number back to digits

The Apple II actually has a routine to display numbers on the screen, but only in hexadecimal. But since we only input decimal numbers, it seemed best that the output should be in decimal as well.

The algorithm to convert a number back to digits is very much atoi (which we saw earlier) in reverse. Here it is in Python:

def itoa(n):
    digits = ''
    while n > 0:
        r = n % 10
        n = int(n / 10)
        digit = chr(ord('0') + r)
        digits = digit + digits
    return digits

The gist is to keep dividing by 10 until the number is 0. The remainder is the digit, and the quotient is the unprocessed portion of the number. Adding 0x30 to a digit will give you the ASCII character code. Somewhat annoyingly, it produces digits in the opposite order they need to be printed in.

This routine prints a 16-bit number in Assembly:

prntDec
    lda #0       ; clear index var
    pha

prntDecLoop
    lda #10      ; set divisor
    jsr div168   ; divide XY by 10

    clc          ; clear carry before add
    adc #$b0     ; add remainder to ascii 0

    stx temp     ; save X in the temp var
    plx          ; pull the index from the stack
    sta buffer,X ; store the digit in the buffer
    inx          ; increase the index
    phx          ; push the index back to the stack
    ldx temp     ; restore X from the temp var

    txa          ; is the lsb > 0?
    bne prntDecLoop
    tya          ; is the msb > 0?
    bne prntDecLoop

    plx          ; pull the loop index

prntDecOutput
    dex          ; decrement the index
    lda buffer,X ; get next character
    jsr cout     ; print the next character

    txa          ; check if X is 0
    bne prntDecOutput

    rts

This code is equivalent to the Python version, except digits are added to a buffer in reverse order, then printed, starting from the back. cout is the routine from the Apple II’s ROM to print a character.

Division

Just like multiplication, the 6502 does not have a division instruction either. We will have to write our own division routine.

Dividing binary numbers by hand is also something reminiscent of grade school. This is 123 divided by 10 by hand:

		 1100 = 12
	 --------
1010 |1111011
      1010
      ----
       1010
       1010
       ----
          011 = 3

Unfortunately, this is tricky to translate into code (at least, I found it hard). But I found an article by Neil Parker with a lovely algorithm for division. Below is the version I adapted for sum (the only difference is that this one takes an 8-bit divisor and can therefore get its input from the registers):

div168
    sta divisor    ; store divisor

    stx dividend   ; store lsb of the dividend
    sty dividend+1 ; store msb of the dividend

    lda #0         ; clear remainder
    sta rem

    ldx #$10       ; 16 bits in our dividend

div168loop
    asl dividend   ; shift lsb of the dividend
    rol dividend+1 ; shift msb of the dividend
    rol rem        ; shift the overflow into the remainder

    lda rem        ; attempt to subtract divisor from rem
    sec            ; set carry before subtraction
    sbc divisor    ; subtract
    bcc div168next ; if rem < divisor, loop again

    sta rem        ; store the result of the subtraction
    inc dividend   ; add a 1 in the result

div168next
    dex
    bne div168loop

    ldx dividend   ; put lsb of quotient in X
    ldy dividend+1 ; put msb of quotient in Y
    lda rem        ; put remainder in A

    rts

I won’t spoil this algorithm by explaining it. I found it elegant, and I will leave it for you to discover yourself.

Thanks for reading. The full source code is on GitHub: sum.s